Auto-Encoding Variational Bayes
1. Abstract
How can we perform efficient inference and learning in directed probabilistic models, in the presence of continuous latent variables with intractable posterior distributions, and large datasets? We introduce a stochastic variational inference and learning algorithm that scales to large datasets and, under some mild differ- entiability conditions, even works in the intractable case.
-
Directed Probabilistic Models: These models, often represented as directed graphical models or Bayesian networks, define a joint probability distribution over a set of variables. In a directed graphical model, each node represents a random variable, and edges represent probabilistic dependencies.The joint probability distribution in a directed graphical model with variables \(X_1, X_2, \ldots, X_n\) \(P(X_1, X_2, ..., X_n) = \prod_{i=1}^{n} P(X_i | \text{Parents}(X_i))\)
-
Continuous Latent Variables: These are variables that are not directly observed and can take any value in a continuous range.
-
Intractable Posterior Distributions: Often in Bayesian inference, we are interested in the posterior distribution of the latent variables given observed data, which is expressed as: \(P(\text{Latent} | \text{Data}) = \frac{P(\text{Data} | \text{Latent}) \times P(\text{Latent})}{P(\text{Data})}\)
However, this distribution is often intractable because the denominator, \(P(\text{Data})\), involves an integral over all possible values of the latent variables which is computationally challenging or even impossible to compute exactly.
2. Method
The strategy in this section can be used to derive a lower bound estimator (a stochastic objective function) for a variety of directed graphical models with continuous latent variables. We will restrict ourselves here to the common case where we have an i.i.d. dataset with latent variables per datapoint, and where we like to perform maximum likelihood (ML) or maximum a posteriori (MAP) inference on the (global) parameters, and variational inference on the latent variables.
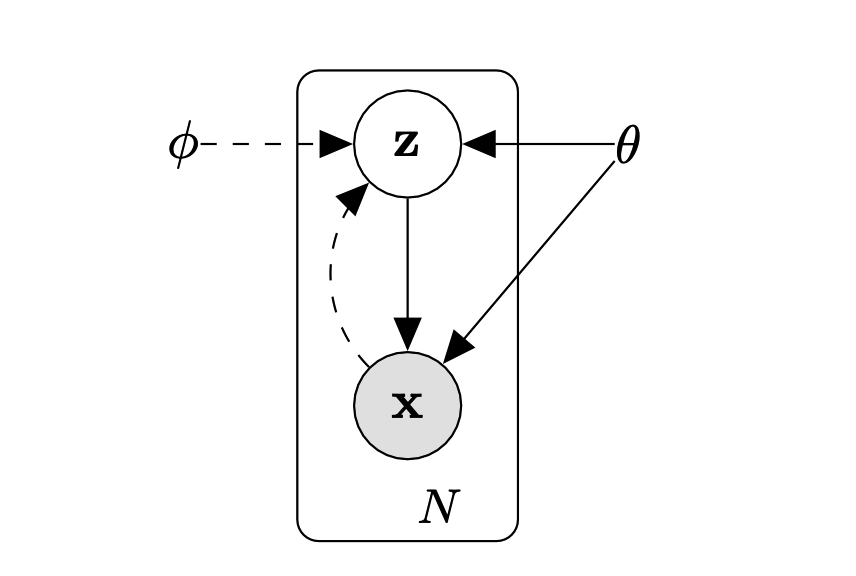
2.1 Problem Scenario
Let us consider some dataset \(X = \{x^{(i)}\}_{i=1}^N\) consisting of \(N\) i.i.d. samples of some continuous or discrete variable \(x\). We assume that the data are generated by some random process, involving an unobserved continuous random variable \(z\). The process consists of two steps:
- A value \(z^{(i)}\) is generated from some prior distribution \(p_{\theta^*}(z)\).
- A value \(x^{(i)}\) is generated from some conditional distribution \(pθ∗ (x/z)\).
We assume that the prior \(p_{\theta^*}(z)\) and likelihood \(p_{\theta^*}(x/z)\) come from parametric families of distributions \(p_{\theta}(z)\) \(p_{\theta}(x/z)\) and that their PDFs are differentiable almost everywhere w.r.t. bot and \({theta}\) and \(z\). Unfortunately, a lot of this process is hidden from our view: the true parameters \(\theta^*\) as well as the values of the latent variables \(z^{(i)}\) are unknown to us.
Very importantly, we do not make the common simplifying assumptions about the marginal or pos- terior probabilities. Conversely, we are here interested in a general algorithm that even works efficiently in the case of:
- Intractability:
- The integral of the marginal likelihood \(p_{\theta}(x) = \int p_{\theta}(z)p_{\theta}(x/z)dz\) is intractable, rendering the evaluation or differentiation of the marginal likelihood impossible.
- The true posterior density \(p_{\theta}(z/x) = \frac{p_{\theta}(x/z)p_{\theta}(z)}{p_{\theta}(x)}\) is intractable, which means that traditional EM algorithms are not applicable.
- Integrals necessary for any reasonable mean-field Variational Bayesian (VB) algorithm are also intractable. These issues are common in cases of moderately complex likelihood functions, such as a neural network with a nonlinear hidden layer.
- Large Datasets:
- When dealing with extensive datasets, batch optimization becomes prohibitively expensive. We prefer to make parameter updates using small minibatches or individual datapoints.
- Sampling-based solutions like Monte Carlo EM are generally too slow since they involve an expensive sampling loop per datapoint.
We are interested in, and propose a solution to, three related problems in the above scenario:
Efficient Approximate ML or MAP Estimation: We aim for an efficient approximate Maximum Likelihood (ML) or Maximum a Posteriori (MAP) estimation for the parameters \(\theta\). The parameters are of interest in their own right, such as when analyzing natural processes, and they allow us to mimic the hidden random process to generate artificial data resembling real data.
Efficient Approximate Posterior Inference: We seek to efficiently infer the latent variable \(z\) given an observed value \(x\) for a chosen set of parameters \(\theta\), useful for coding or data representation tasks.
Efficient Approximate Marginal Inference: Our goal is to perform efficient marginal inference of the variable \(x\), enabling various inference tasks where a prior over \(x\) is needed, with applications in computer vision like image denoising, inpainting, and super-resolution.
To tackle the aforementioned challenges, we introduce a recognition model \(q_{\phi}(z/x)\) : an approximation to the intractable true posterior \(p_{\theta}(z/x)\). Unlike the approximate posterior in mean-field variational inference, our recognition model is not necessarily factorial, and its parameters \(\phi\) are not derived from some closed-form expectation. Instead, we propose a method for learning the recognition model parameters \(\phi\) jointly with the generative model parameters \(\theta\).
From a coding theory perspective, the unobserved variables \(z\) can be seen as a latent representation or code. Hence, we refer to the recognition model \(q_{\phi}(z/x)\) as a probabilistic encoder, which, given a datapoint \(x\), produces a distribution over the potential codes \(z\). Conversely, we refer to \(p_{\theta}(x/z)\) as a probabilistic decoder, as it yields a distribution over the potential corresponding values of \(x\) given a code \(z\).
2.2 The Variational Bound
In the study of variational inference, a pivotal concept is that of the variational bound. The marginal likelihood of our dataset can be decomposed into a sum over the marginal likelihoods of individual data points:
\[\log p_{\theta}(x^{(1)}, \ldots, x^{(N)}) = \sum_{i=1}^N \log p_{\theta}(x^{(i)}),\]which provides us with an individualized view of the dataset, focusing on one data point at a time. For each data point, the log likelihood can be expressed in a way that reveals a crucial relationship:
\[\log p_{\theta}(x^{(i)}) = D_{KL}(q_{\phi}(z/x^{(i)}) \parallel p_{\theta}(z/x^{(i)})) + \mathcal{L}(\theta, \phi; x^{(i)}) \tag{1}\]Here, the first term on the right-hand side (RHS) is the Kullback-Leibler (KL) divergence between the approximate and the true posterior distributions. Given that KL divergence is always non-negative, the second term, \(\mathcal{L}(\theta, \phi; x^{(i)})\), emerges as a lower bound on the marginal likelihood for data point \(i\), known as the (variational) lower bound.
And an alternative formulation of the lower bound, focusing on the KL divergence and the expected log likelihood, is given by:
\[\mathcal{L}(\theta, \phi; x^{(i)}) = -D_{KL}(q_{\phi}(z/x^{(i)}) \parallel p_{\theta}(z)) + \mathbb{E}_{q_{\phi}(z/x^{(i)})} \left[ \log p_{\theta}(x^{(i)}/z) \right] \tag{3}\]Our goal is to differentiate and optimize this lower bound \(\mathcal{L}(\theta, \phi; x^{(i)})\) with respect to both the variational parameters \(\phi\) and the generative parameters \(\theta\). However, computing the gradient of the lower bound with respect to \(\phi\) poses challenges. The typical Monte Carlo gradient estimator for this kind of problem is high variance and not practical for our purposes:
\[\nabla_{\phi} \mathbb{E}_{q_{\phi}(z)} [f(z)] = \mathbb{E}_{q_{\phi}(z)} \left[ f(z) \nabla_{\phi} \log q_{\phi}(z) \right] \approx \frac{1}{L} \sum_{l=1}^L f(z^{(l)}) \nabla_{\phi} \log q_{\phi}(z^{(l)})\]where \(z^{(l)} \sim q_{\phi}(z/x^{(i)})\). The estimator’s high variance is a major obstacle, as it makes the optimization process inefficient and unstable.
Insight: The crux of our approach is to harness a more efficient gradient estimator, reducing variance and enabling practical application to large-scale datasets. This is where advanced techniques come into play, which we will explore in the subsequent sections.
Ronak
Mathematically, a convolution operation in a CNN can be represented as:
\[f(x, y) = \sum_{i=-a}^{a} \sum_{j=-b}^{b} K(i, j) \cdot I(x-i, y-j)\]Here, ( f(x, y) ) is the output after applying the convolution operation to the input image ( I ) at position ( (x, y) ). The kernel ( K(i, j) ) is applied over the image such that each element of the kernel is multiplied by the corresponding element of the image under it, and the results are summed to produce the output ( f(x, y) ). The kernel ( K ) can be expressed as a matrix:
\[K = \begin{bmatrix} k_{11} & k_{12} & k_{13} \\ k_{21} & k_{22} & k_{23} \\ k_{31} & k_{32} & k_{33} \end{bmatrix}\]With fewer parameters than fully connected networks, CNNs can learn hierarchical representations of images thanks to these principles, which makes them particularly useful for tasks like object detection and image classification.
2. Dataset
ImageNet is a dataset of over 15 million labeled high-resolution images belonging to roughly 22,000 categories.
3. The Architecture
3.1 ReLU Nonlinearity
In terms of training time with gradient descent, these saturating nonlinearities are much slower than the non-saturating nonlinearity f(x) = max(0,x). Following Nair and Hinton [20], we refer to neurons with this nonlinearity as Rectified Linear Units (ReLUs). Deep convolutional neural net- works with ReLUs train several times faster than their equivalents with tanh units.
The activation function is a core component in neural networks that introduces non-linearity, affecting the network’s ability to learn complex patterns. Traditional activation functions like the hyperbolic tangent (tanh) or the sigmoid function can cause the gradient to vanish during backpropagation, which slows down the training.
The Rectified Linear Unit (ReLU) has become the de facto standard in neural network activation due to its non-saturating form, defined as:
\[ReLU(x) = \max(0, x)\]This simple yet powerful function maintains the gradient, preventing the vanishing gradient problem and allowing the network to learn faster. Neurons with ReLU activation are only activated when the input is positive, leading to sparse activation within the network.
CNNs with ReLUs train substantially faster than those with tanh units. This efficiency gain is depicted in the figure below, which demonstrates how a four-layer convolutional network with ReLUs can reach a 25% training error rate on CIFAR-10 much quicker than the same network utilizing tanh neurons.
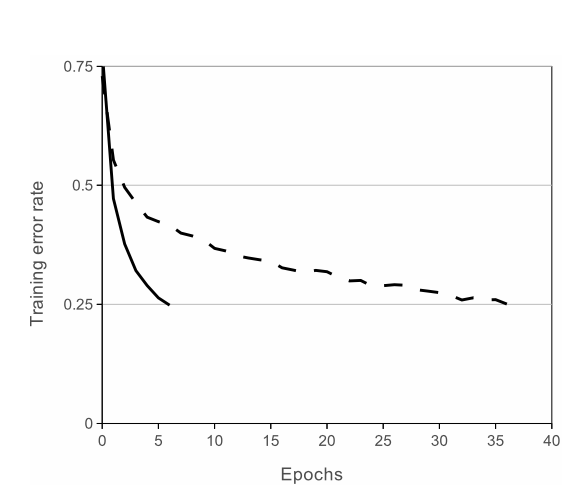
Empirical results show that networks with ReLU not only train faster but also achieve better performance on complex tasks, which is particularly beneficial when dealing with large datasets and deep architectures.
3.3 Local Response Normalization
ReLUs have the desirable property that they do not require input normalization to prevent them from saturating. If at least some training examples produce a positive input to a ReLU, learning will happen in that neuron. However, we still find that the following local normalization scheme aids generalization.
The Role in ReLU Networks
While Rectified Linear Units (ReLUs) have the advantage of not requiring input normalization to prevent saturation, we discovered an additional normalization technique that enhances generalization. This is known as Local Response Normalization (LRN).
Mechanism of LRN
Given the activity \(a*{i}^{x,y}\) of a neuron, calculated by applying \(kernel ( i )\) at position \((x, y)\) and then passing it through a ReLU nonlinearity, the response-normalized activity \(( b*{i}^{x,y} )\) can be described by:
\[b_{i}^{x,y} = \frac{a_{i}^{x,y}}{\left(k + \alpha \sum_{j=\max(0, i-n/2)}^{\min(N-1, i+n/2)} (a_{j}^{x,y})^2\right)^\beta}\]Here, the sum runs over ( n ) “adjacent” kernel maps at the same spatial position, and ( N ) represents the total number of kernels in the layer. This normalization is inspired by lateral inhibition found in biological neurons, inducing competition among neuron outputs computed with different kernels.
3.4 Overlapping Pooling
If a pooling layer has a grid of pooling units, they are spaced s pixels apart and each summarizes a z × z neighborhood. Traditional pooling sets s = z, meaning no overlap between the neighborhoods.
However, Imagenet employs an overlapping pooling strategy. They set s < z. Specifically, we use s = 2 and z = 3. This overlapping approach has been found to be more effective in reducing error rates.
3.5 Overall Architecture
As depicted in Figure 2, the net contains eight layers with weights; the first five are convolutional and the remaining three are fully- connected. The output of the last fully-connected layer is fed to a 1000-way softmax which produces a distribution over the 1000 class labels. Our network maximizes the multinomial logistic regression objective, which is equivalent to maximizing the average across training cases of the log-probability of the correct label under the prediction distribution.
The approximately 60 million trainable parameters of Imagenet are a crucial component. This large number of parameters improves the network’s classification performance by enabling it to learn intricate and subtle features from the vast and diverse ImageNet dataset. Throughout the training phase, these parameters are changed to allow the network to perform as well as possible on the dataset.
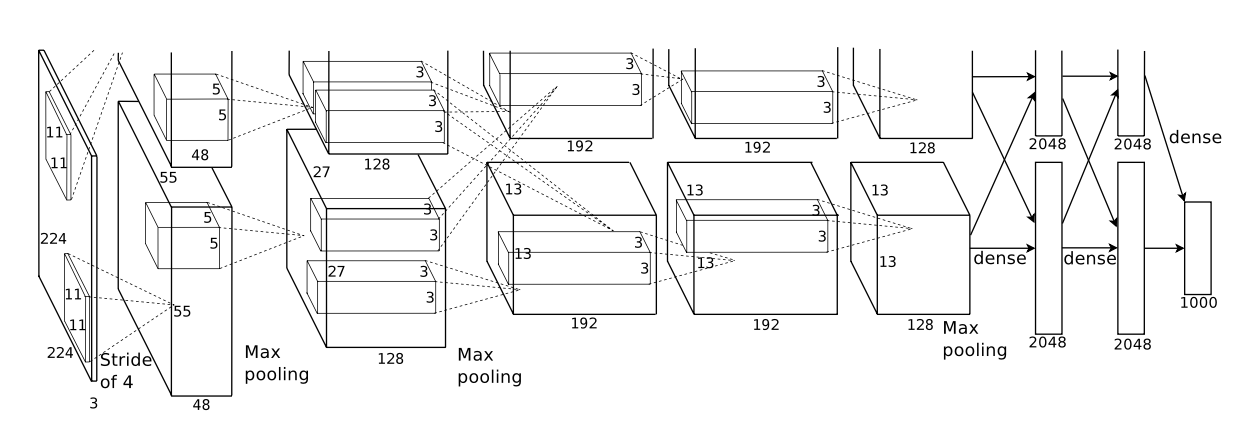
Imagenet(
(features): Sequential(
(0): Conv2d(3, 64, kernel_size=(11, 11), stride=(4, 4), padding=(2, 2)) // 23,232 parameters
(1): ReLU(inplace=True)
(2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(64, 192, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) // 307,200 parameters
(4): ReLU(inplace=True)
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Conv2d(192, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) // 663,552 parameters
(7): ReLU(inplace=True)
(8): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) // 884,736 parameters
(9): ReLU(inplace=True)
(10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) // 589,824 parameters
(11): ReLU(inplace=True)
(12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(avgpool): AdaptiveAvgPool2d(output_size=(6, 6))
(classifier): Sequential(
(0): Dropout(p=0.5, inplace=False)
(1): Linear(in_features=9216, out_features=4096, bias=True) // 37,748,736 parameters
(2): ReLU(inplace=True)
(3): Dropout(p=0.5, inplace=False)
(4): Linear(in_features=4096, out_features=4096, bias=True) // 16,777,216 parameters
(5): ReLU(inplace=True)
(6): Linear(in_features=4096, out_features=1000, bias=True) // 4,096,000 parameters
)
)
4 Reducing Overfitting
Our neural network architecture has 60 million parameters. Although the 1000 classes of ILSVRC make each training example impose 10 bits of constraint on the mapping from image to label, this turns out to be insufficient to learn so many parameters without considerable overfitting. Below, we describe the two primary ways in which we combat overfitting.
4.1 Data Augmentation
We employ two distinct forms of data augmentation
- Generating image translations and horizontal reflections
- PCA Color Augmentation
PCA Color Augmentation
PCA Color Augmentation is a technique to augment image data by adjusting the intensities of the RGB channels. This method helps the model become more invariant to changes in illumination, which is a common property of natural images.
The process involves the following steps:
- Perform PCA on the RGB pixel values across the entire ImageNet training set to obtain principal components.
- For each training image, alter the pixel values by adding a certain amount of these principal components.
Mathematically, for each pixel \(I\_{xy} = [I_R, I_G, I_B]^T\) in the image, we add the following quantity:
\[[p_1, p_2, p_3][\alpha_1 \lambda_1, \alpha_2 \lambda_2, \alpha_3 \lambda_3]^T\]Here:
- \(p_i\) represents the \(i\)-th eigenvector from the PCA of the RGB pixel values.
- \(\lambda_i\) is the corresponding eigenvalue, which indicates the variance in the direction of the eigenvector.
- \(\alpha_i\) is a random variable drawn from a Gaussian distribution with mean zero and standard deviation 0.1. It is sampled once per image and used across all pixels, ensuring consistency within the image.
By scaling the principal components by their corresponding eigenvalues and the random variable, we effectively simulate realistic variations in lighting. This adjustment to the pixel values does not alter the content or structure of the image, preserving the label of the image while providing a form of regularization.
4.2 Dropout
The recently-introduced technique, called “dropout” [10], consists of setting to zero the output of each hidden neuron with probability 0.5. The neurons which are “dropped out” in this way do not contribute to the forward pass and do not participate in back- propagation. So every time an input is presented, the neural network samples a different architecture, but all these architectures share weights. This technique reduces complex co-adaptations of neurons, since a neuron cannot rely on the presence of particular other neurons. It is, therefore, forced to learn more robust features that are useful in conjunction with many different random subsets of the other neurons.
To stop overfitting in neural networks, dropout is a regularization technique used. The network is forced to learn robust features that are independent of any particular set of neurons by randomly setting a portion of the neuron outputs to zero during training. Overfitting is essentially reduced by the randomness in neuron activation, which improves the model’s ability to generalize to new data. Neuron outputs are adjusted to compensate for the deactivated neurons during training, but dropout is not applied during testing.
Results
Comparison of Model Performances
The paper presents a comparison of the convolutional neural network (CNN) model with other notable methods. Below is a summary of their performances on the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) for the years 2010 and 2012:
| Model | Top-1 Error (ILSVRC-2010) | Top-5 Error (ILSVRC-2010) | Top-5 Error (ILSVRC-2012) |
|---|---|---|---|
| CNN | 37.5% | 17.0% | 15.3% |
| Sparse Coding [2] | 47.1% | 28.2% | 26.2% (val) |
| SIFT + FVs [24] | 45.7% | 25.7% | - |
Analysis
- CNN: Demonstrates a notable decrease in the top-1 and top-5 error rates. This demonstrates how deep convolutional neural networks work well for tasks involving image classification.
- Sparse Coding [2]: Even though it works well, this approach has higher error rates than CNN, which highlights how much better deep learning techniques perform.
- SIFT + FVs [24]: It shows higher error rates, just like Sparse Coding. The comparison demonstrates how CNNs have improved at handling challenging image recognition tasks.
This comparative analysis illustrates the groundbreaking impact of CNNs in reducing error rates and setting new benchmarks in image classification.
Conclusion
By utilizing the expansive ImageNet dataset, the network achieved remarkable accuracy, showcasing a significant leap over previous state-of-the-art results. Key innovations include the use of ReLU nonlinearity, dropout for overfitting reduction, and extensive data augmentation, contributing to the network’s robust performance.
Citation
Krizhevsky, A., Sutskever, I., & Hinton, G. E. (2012). ImageNet Classification with Deep Convolutional Neural Networks. NIPS.